光的色散實驗
實驗十二
利用稜鏡分光的特性，測量不同入射光波長對稜鏡折射率的關係。
原理
由於稜鏡的折射率n(λ)與入射光的波長λ有關，所以不同波長的入射光，在稜鏡內部走的路徑一定不會相同。當非單一波長的光源傾斜入射至稜鏡時，不同波長的光會被散開，這就是所謂光的色散（chromatic dispersion）。（如下圖）
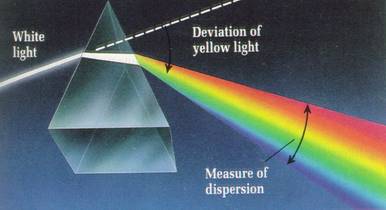
藉由此性質我們可以將非單色光源分光。至於光走的實際路徑，可由折射定率【見附錄二】決定。
折射定率： 
(1)
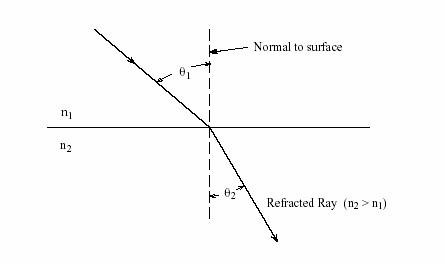
n1、n2代表不同介質的折射率，θ1、θ2分別表示入射角與折射角
接著利用此簡單定律，計算三稜鏡對於入射光線所產生的的偏離角度（deviation angle）。只要利用兩次折射定律及幾何角度的關係，就可以得到下列結果。
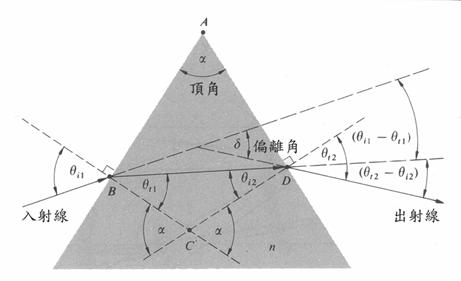
δ為偏離角，
、 
為入射角、 
、 
為折射角。
由上圖可看出
由四邊形ABCD中可看出
，其中a為三菱鏡的頂角
所以
根據折射定律(1)可得到
即可得 
(2)
n(λ)為稜鏡的折射率【注意：為入射光波長的函數】首先將已知兩種不同波長的單色光射入至三稜鏡，經過兩次折射回到空氣中，由於不同波長的單色光其偏離角度不同，所以分散在不同的角度方向上，其它未知波長的位置則由線性的內外差法決定。
附錄一
某些物質，折射率與入射光波長的關係
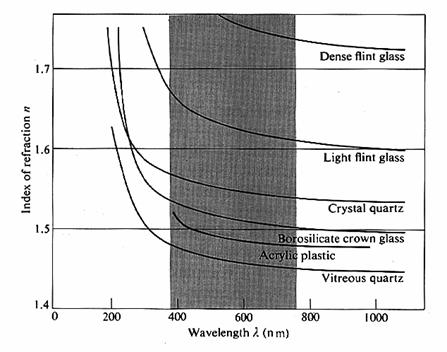
附錄二
1.惠更斯原理(Huygens』 principle)
假設波前(wave front：ab)上的每一點，可以視為二級的波列(wavelets)源，然後以原來波動速率（在同一介質中）向四面八方傳播，新的波前（de）與二級的波列源相切，成為其波包(envelope)。此原理可以簡單的幾何來決定，下一個時刻波前的形狀。
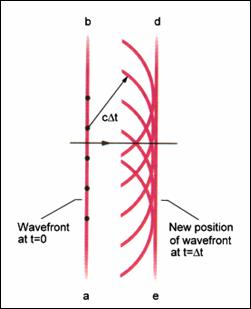
2.利用惠更斯原理來證明折射定率：
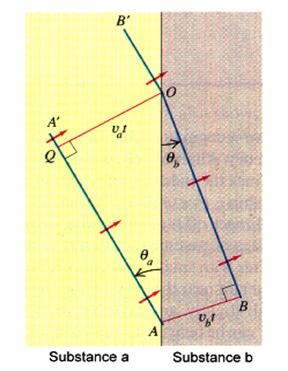
假設某一個波前（ 
）從介質a（折射率 
）往介質b（折射率 
）傳播，A在恰好在交界面上
，利用惠更斯原理來找t時間後透射波波前的位置（OB），二級的波列Q經過時間t球面波的半徑為
t，而二級的波列A經過時間t球面波的半徑為 
t，假設波前進的方向（與波前垂直）與界面法線
的夾角為 
、 
，及入射角為 ，反射角為 ，則下圖中 
、 
。利用簡
單的三角幾何得知 
，合併得 
。藉由折射率的定義
（c為光速），改寫成 
或為 
。
儀器與裝置
汞燈(含木板)1組，底座和支架2組，稜鏡1個，狹縫片1片，可轉方桌1個，屏幕1 個，手電筒2支，捲尺、長尺及短尺各一支，三角板一組，布織手套一副
儀器架設
儀器架設圖：(A)汞燈；(B)狹縫；(C)稜鏡；(D)可旋轉黑色方桌；(E)屏幕
實驗步驟 1.
儀器架設如上圖所示，移動支撐黑色方桌的底座使黃銅柱對準圓盤刻度中心，再將稜鏡小心置於方桌中心處，使稜鏡其中一邊與附有指針之桌邊平行(如下圖)。 2.
調整木板上的螺絲，即調整汞燈高度使光平行射出，之後調整狹縫的高度並對準其位置，確定汞燈發出的光可通過此狹縫，再調整上圖之裝置，使光束沿指針方向垂直射入稜鏡面的中心。 3.
改變光束的入射角大小，即旋轉方桌(因方桌套在黃銅柱上，握住連接桌面之黑色管柱，即可轉動桌面)，直至可清楚看到分光現象，出現黃、藍綠、紫三條不同顏色的光束為止，記錄此時入射角角度。 4.
在屏幕上點出黃、藍綠、紫三條光束的位置，連線回到圓盤刻度上，即可算出入射光束與出射光束的角度差，也就是偏離角的大小。 5.
將測得的入射角大小及各條光束的偏離角大小，代入(2)式，分別求出各條光束對應的稜鏡折射率大小。
6. 參照講義上各種色光所對應的波長，作折射率
預習問題 1. 推導第(2)式。
實驗紀錄 入射角 波長 偏離角 稜鏡折射率 黃光 藍綠光 紫光 作折射率
思考問題 1. 將我們求得的 2. 假設有一凸透鏡，其兩面的曲率半徑皆為15cm且其材質和我們實驗中使用的稜鏡相同。今有一如下圖的實驗裝置，求當汞燈的兩平行光束通過凸透鏡後，其紅色光、黃色光、綠色光及紫色光分別對應的焦距
對波長 
的關係圖： 
，求 
、 
、 
值各為何。 :___________
; 頂角a:____________
對波長 的關係圖： ，
=__________， =__________，
=____________。 、 、 值代入 中，可得出汞燈的黃色光及藍綠色光所對應的稜鏡折射率應分別為何？
各為何？提示：造鏡者公式
