實驗八 雷射光學實驗
目的
觀察光通過單狹縫時所產生的繞射現象，並測量亮、暗紋的位置和理論值相比較。
原理
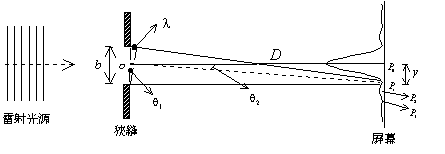
當光通過一單狹縫時，如縫愈窄則光線會愈向兩旁擴張，此現象即所謂的繞射。一平行光源通過狹縫時所產生的繞射
現象稱為，Fraunhofer 繞射，非平行光源通過狹縫時所產生的繞射現象我們稱為 Fresnel 繞射。繞射現象的產生我們可
依據惠更斯原(即波前上的每個點，可被當作二次子波的起始點)，獲得圓滿的解釋。簡單討論如下：令狹縫的寬度為 b，
中心點為 
點，狹縫口被均分成若幹點，如圖１所示。
點光程差為零，稱為中央亮區。
點至狹縫頂點的距離比到
狹縫底點的距離大一波長
，亦就是說 
點到狹縫頂點的距離，比
點到 
點的距離大半波長（
），所以狹縫
頂點發出的二次子波與由 
點發出的二次子波在
點的光程差（
），干涉結果強度為零。同理狹縫頂點以下第一
點和 
點以下第一點的光程差也為半波長，故在
點其強度亦為零。如此，兩兩相對，整個狹縫的二次子波在
點
皆干涉為零，因此 
點為一暗點。依此類推，
點至狹縫頂、底兩端的光程為
2 倍波長，我們將狹縫寬分為四段，則
可知全部效應又干涉為零，所以 
點亦為一暗點。而
點至狹縫上、下兩端點的光程差是
，將狹縫度分為三段，
則兩段干涉為零，另一段的效果是強度相加，故 
點為一亮區。綜合以上分析，得出當
光程差
，
時為暗區；
光程差
，
時為亮區。
因為 
甚小，
即 
，故
亦即
，
(1)
亦即
，
(2)
以上僅是較粗略的說明。對一平行光源而言，較嚴謹的教學推導可參考【Francis A. Jenkins and Harvey
E. White (1976). Fundamentals of Optics, Fourth Edition, P316~322.】。由其推導結果可知
(2) 式只是一趨近式，事實上繞射條紋的亮區是發生在
等位置上。
 |
|
圖１
|
儀器與裝置
雷射光源、單狹縫片、底座和支架（×2）、紙屏幕、15 cm 短尺、捲尺。
 |
|
圖２ 儀器裝置圖
|
步驟
| 注意事項： |
| a. 不可將雷射光照射別人的眼睛。 |
| b. 仔細清理整理盒內各狹縫等之數目。 |
| c. 將狹縫置於支架上，或取下時要小心，以防止狹縫片破損，且實驗前後值仔細檢查是否有破損現象。 |
| d. 狹縫與光行進方向須垂直。 |
1. 將實驗器材配置如圖２所示。
2. 移開狹縫片使光直接照射在紙屏上，並用鉛筆在紙屏上的亮點寫上「
」記 號。
3. 置放狹縫片於雷射前，且左右移動狹縫，使雷射光源正射於狹縫上。
4. 用鉛筆把紙屏上的亮、暗條紋的位置畫記號。
5. 以捲尺量出狹縫至紙屏的距離 D。
6. 利用 15 cm 的短尺量出各亮、暗條紋中心至 
點的距離 y，並用
(1)、(2)式計算出 y 之理論值。
7. 以兩刀片代替狹縫，並調整狹縫寬度，觀察其繞射條紋的變化。
預習問題
1. 產生 Fraunhofer 繞射的條件是什麼？
2. 產生 Fresnel 繞射的條件是什麼？
記錄
1. 狹縫寬 b =_____________ mm；D =______________
mm；
。
2.
|
區中心名稱
|
使用公式
|
n
|
y 理論值
|
y 實驗值
|
|
右第一暗區中心
|
(1)
|
1
|
||
|
右第一亮區中心
|
(2)
|
1
|
||
|
右第二暗區中心
|
(1)
|
2
|
||
|
右第二亮區中心
|
(2)
|
2
|
3. 各亮、暗區的寬度
|
中央亮區寬度
|
單位（mm）
|
|
右邊第一亮區寬度
|
|
|
右邊第二亮區寬度
|
|
|
左邊第一亮區寬度
|
|
|
左邊第二亮區寬度
|
|
思考問題
1. 中央亮區之寬度是否等於第一亮區寬度的 2 倍？為什麼？
2. 當狹縫寬度改變時，繞射條紋有何變化？
3. 繞射之亮、暗紋位置 
之理論值與實驗值之誤差為何？
4. 若雷射光之波長改變，則繞射條紋有何變化？
目的
觀察光入射在障礙物邊緣時所產生的繞射現象。
原理
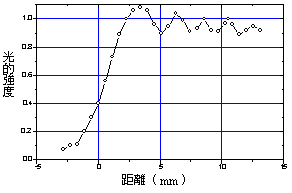
幾何光學中認為光是沿直線前進，但若仔細觀察光在障礙物後面所造成的陰影時，就會發現光也有繞射的現象，亦即光亦應具有波動性。如用一個銳利的刀口擋住雷射光束的一部分，則被刀口擋住部分的後面並不是完全黑暗，仍然有一部分光未被擋住而繞射進去；且在未被擋住部分的附近一帶，光也因繞射現象強度變得不相同形成繞射條紋，詳細見圖３所示。因其理論太繁雜在此不予討論，有興趣者可參考【Francis A. Jenkins and Harvey E. White (1976), Fundamentals of Optics, Fourth Edition, P388~396.】。
 |
|
圖３ 光通過障礙物邊緣後其強度分佈圖
|
儀器與裝置
雷射光源、刀片、底座和支架、紙屏幕。
步驟
| 注意事項： |
| a. 不可將雷射光照射別人的眼睛。 |
1. 將雷射光源與紙屏幕相距約 1.3 米。
2. 把一片刀片置於支架上，然後置於雷射光前方，並左右移動位置使雷射光束 被刀口擋住一半。
3. 觀察紙屏上的繞射現象，並用筆畫下它的大概圖形。
預習問題
1. 各舉一例說明光具粒子性或波動性。
記錄
在實驗報告紙上畫出邊緣繞射的圖形。
思考問題
1. 你是否能由肉眼判斷出光通過障礙物邊緣後，在末被障礙物遮蔽處附近的繞射現象。若不能則應如何驗證呢？
目的
觀察光通過雙狹縫後所產生的繞射及干涉條紋，並利用此條紋之測量出雷射光源的波長。
原理
 |
|
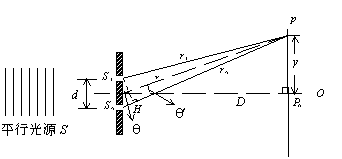
圖４ 雙狹縫實驗
|
如圖４所示。設有一平行光源 S 照射在一狹縫寬度 b，且兩狹縫中心點的相距距離
d 的雙狹縫後，投射在屏幕上之 P 點。則 P 點的光強度
(3)
其中 
，
，詳細情形請參考【Francis
A. Jenkins and Harvey E. White (1976), Fundamentals of Optics, Fourth Edition,
P339~341.】。
(3) 式中 
是表繞射因子，
是表干涉因子。因此由
(3) 式可知 P 點為暗區（暗紋）的條件是
，
(4)
及 
，
(5)
而此條件乃某一亮區內令有許多干涉條紋的原因。若實驗時 
則 
近似一等腰三角形，所以
；且因 
和很小，所以 
，
，故 
，因此 (4) 式及 (5)
式可改寫為
，
(6)
和 
，
(7)
但 (3) 式中 
之極大值之正確位置
y 較難以一簡單的關係表示。然而，其近似的位置我們可以略去因子
而求之，亦就是 
當極大的條件，可以僅決定於因子
故若符合
，
(8)
即 
，
（極大） (9)
時，
就會有極大值產生。
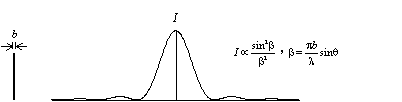
綜合以上討論可知，當光通過一雙狹縫後，不僅會產生干涉現象，同時亦會產生繞射現象，詳細情形見圖５所示。
 |
|
(a) 單狹縫的繞射
|
 |
|
(b) 雙狹縫的干涉
|
 |
|
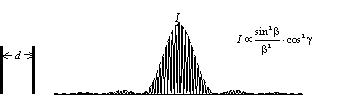(c) 雙狹縫的繞射與干涉
|
|
圖５ 光通過雙狹縫後的繞射及干涉圖
|
儀器與裝置
雷射光源、雙狹縫片、紙屏幕、底座和支架（×2），15 cm 短尺捲尺。
步驟
| 注意事項： |
| a. 不可將雷射光照射別人的眼睛。 |
| b. 仔細清理整理盒內各狹縫等之數目。 |
| c. 將狹縫置於支架上，或取下時要小心，以防止狹縫片破損，且實驗前後值 仔細檢查是否有破損現象。 |
1. 將屏幕置放在雷射光源前方約 1.3 m 處。
2. 打開雷射光源，使雷射光打在屏幕中央，然後用鉛筆在屏幕上的亮點中央記 上「
」記號。
3. 把雙狹縫放置於雷射光源前方使狹縫與光行進方向重疊，並在左右移動雙狹 縫位置，使屏幕上出現明顯的干涉、及繞射條紋，將此一圖 形記錄下來。
4. 用捲尺量出雙狹縫到屏幕的距離 D。
5. 用短尺量出各亮暗條紋到 
點的距離y。
6. 利用 (6)、(7)、(9) 式計算雷射光的波長 
。
預習問題
1. 何謂繞射？何謂干涉？它們之間的區別為何？
記錄
1. b =_______________mm；d =_______________mm；D =_______________mm。
|
條紋名稱
|
長度(mm)
|
m 值
|
雷射光波長
 (m)
|
|
中央極大亮數
|
|
|
|
|
左端第一亮數
|
|
|
|
|
右端第一亮數
|
|
|
|
|
左端第二暗數
|
|
|
|
|
右端第二暗數
|
|
|
|
|
左端第二亮數
|
|
|
|
|
右端第二亮數
|
|
|
|
平均值
=_______________ m。
思考問題
1. 若雷射光的波長改變，則繞射及干涉條紋有何變化？
2. 波長 
的光，入射在兩縫中心相距 0.02
mm 的雙狹縫上，且雙狹縫距屏幕的距離為 80.0 cm，求干涉帶之寬度。
3. 利用雙狹縫實驗所求出的雷射光波長，與雷射光之實際波長的百分誤差為何？
目的
觀察多狹縫及光柵的繞射現象，並利用光柵繞射求出雷射光的波長。
原理
當光透過一系列寬度相同、互相平行且等距離的多狹縫後，會形成一系列相同的繞射條紋。若狹縫之間的距離很小，這一系列的光束會重疊而互相干涉，使繞射條紋裡出現非常狹窄的干涉亮紋。當狹縫的數目極多時，主要的干涉亮紋會變得非常狹窄而明亮次要干涉亮紋會變得微弱而不可見，如圖六所示。也就是說，這時候光被集中到狹窄的亮紋上，這個特性可以利用來分析光譜。而主要亮紋的位置可由下面公式來推算，詳細請參考【Francis
A. Jenkins and Harvey E. White (1976), Fundamentals of Optics, Fourth Edition,
P357~359.】。
，
(10)
其中 d 是鄰近兩狹縫的中心相距之距離，
是第 m
條主要干涉亮紋與光柵中央的連線和入射光之間的夾角。
 |
|
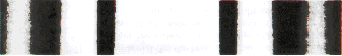(a)單狹縫繞射
|
 |
|
(b)雙狹縫繞射
|
 |
|
(c)多狹縫干涉
|
|
圖６ 光通過各種狹縫時的繞射及干射圖形
|
儀器與裝置
雷射光源，三狹縫、四狹縫、五狹縫、六狹縫、80 lines/mm 與 300 lines/mm 光柵，底座及支架（×2）。
步驟
| 注意事項： |
| a. 不可將雷射光照射別人的眼睛。 |
| b. 仔細清理整理盒內各狹縫等之數目。 |
| c. 將狹縫置於支架上，或取下時要小心，以防止狹縫片破損，且實驗前後值 仔細檢查是否有破損現象。 |
1. 將雷射光直射到約 1.3 米遠的紙屏上，並作「
」記號。
2. 將三狹縫置於雷射光前方。
3. 調整三狹縫位置使牆上的繞射、干涉條紋非常清晰。
4. 觀察並記錄其圖形。
5. 依次更換 4~6 狹縫，並重複步驟 1 ~ 4。
6. 更換多狹縫為光柵，並使紙屏與雷射光源間距離約為 13 米且定出 
點。
7. 觀察圖形，並量出光通過光柵時，其亮點中心至 
點的距離。
8. 利用捲尺測量光柵至紙屏的距離 D。
9. 利用公式 (10) 求出雷射光的平均波長。
預習問題
1. 當光通過的狹縫數愈多時，其繞射及干涉條紋有何變化？
記錄
d =_______________mm；D =_______________m。
|
亮點名稱
|
各亮點至
 之距離(cm) |
m
|
 |
 (m) |
|
左第一亮點
|
|
|
|
|
|
左第二亮點
|
|
|
|
|
|
右第一亮點
|
|
|
|
|
|
右第二亮點
|
|
|
|
|
平均值=_______________
m。
思考問題
1. 利用光柵所求出的雷射光平均波長，與雷射光的實際波長其百分誤差為何？